import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
cmap = ListedColormap(['#FF0000','#00FF00','#0000FF'])
iris = datasets.load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1234)
plt.figure()
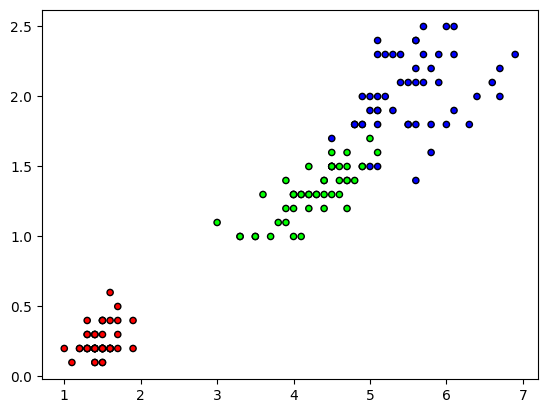
plt.scatter(X[:,2],X[:,3], c=y, cmap=cmap, edgecolor='k', s=20)
plt.show()
from collections import Counter
def euclidean_distance(x1, x2):
np.sqrt(np.sum((x1-x2)**2))
class KNN:
def __init__(self, k=3):
self.k = k
def fit(self, X, y):
self.X_train = X
self.y_train = y
def predict(self, X):
predictions = [self._predict(x) for x in X]
return predictions
def _predict(self, x):
# conmpute the distance
distances = [euclidean_distance(x, x_train) for x_train in self.X_train]
# get the closest k
k_indices = np.argsort(distances)[:self.k]
k_nearest_labels = [self.y_train[i] for i in k_indices]
return predictions
# majority vote
most_common = Counter(k_nearest_labels).most_common()
return most_common[0][0]
from collections import Counter
import numpy as np
def euclidean_distance(x1, x2):
return np.sqrt(np.sum((x1 - x2) ** 2))
class KNN:
def __init__(self, k=3):
self.k = k
def fit(self, X, y):
self.X_train = X
self.y_train = y
def predict(self, X):
predictions = [self._predict(x) for x in X]
return predictions
def _predict(self, x):
# Compute the distance
distances = [euclidean_distance(x, x_train) for x_train in self.X_train]
# Get the closest k indices
k_indices = np.argsort(distances)[:self.k]
# Get the labels of the k nearest neighbors
k_nearest_labels = [self.y_train[i] for i in k_indices]
# Majority vote, most common class label
most_common = Counter(k_nearest_labels).most_common()
return most_common # Return the most common labelclf = KNN(k=5)
clf.fit(X_train, y_train)
predictions = clf.predict(X_test)
print(predictions)[[(1, 4), (2, 1)], [(2, 3), (1, 2)], [(2, 5)], [(0, 5)], [(1, 5)], [(0, 5)], [(0, 5)], [(0, 5)], [(1, 5)], [(2, 5)], [(1, 5)], [(0, 5)], [(2, 5)], [(1, 5)], [(0, 5)], [(1, 5)], [(2, 5)], [(0, 5)], [(2, 5)], [(1, 5)], [(1, 5)], [(1, 5)], [(1, 5)], [(1, 5)], [(2, 5)], [(0, 5)], [(2, 4), (1, 1)], [(1, 5)], [(2, 5)], [(0, 5)]]from collections import Counter
import numpy as np
def euclidean_distance(x1, x2):
return np.sqrt(np.sum((x1 - x2) ** 2))
class KNN:
def __init__(self, k=3):
self.k = k
def fit(self, X, y):
self.X_train = X
self.y_train = y
def predict(self, X):
predictions = [self._predict(x) for x in X]
return predictions
def _predict(self, x):
# Compute the distance
distances = [euclidean_distance(x, x_train) for x_train in self.X_train]
# Get the closest k indices
k_indices = np.argsort(distances)[:self.k]
# Get the labels of the k nearest neighbors
k_nearest_labels = [self.y_train[i] for i in k_indices]
# Majority vote, most common class label
# refining the class to get the first label
most_common = Counter(k_nearest_labels).most_common()
return most_common[0][0] # Return the most common labelclf = KNN(k=5)
clf.fit(X_train, y_train)
predictions = clf.predict(X_test)
print(predictions)[1, 2, 2, 0, 1, 0, 0, 0, 1, 2, 1, 0, 2, 1, 0, 1, 2, 0, 2, 1, 1, 1, 1, 1, 2, 0, 2, 1, 2, 0]# calculating the accuracy
acc = np.sum(predictions == y_test) / len(y_test)
print(acc)0.9666666666666667Resources:-