Homepage - Numpy

NumPy

numerical python - function description
ndarray- multidimensional array providing fast arithmetic operations
mathematical functions
tools for reading/writing
linear algebra, random number generation, fourier transformation

import numpy as np

my_arr = np.arange(1000000)
my_list = list(range(100000))

%timeit my_arr2 = my_arr * 2

3.91 ms ± 154 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

%timeit my_list2 = [x * 2 for x in my_list]

12.3 ms ± 4.77 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

data  = np.array([[1.5, -0.1, 3], [0, -3, 6.5]])

data

array([[ 1.5, -0.1,  3. ],
       [ 0. , -3. ,  6.5]])

data * 10

array([[ 15.,  -1.,  30.],
       [  0., -30.,  65.]])

data + data

array([[ 3. , -0.2,  6. ],
       [ 0. , -6. , 13. ]])

data.shape

(2, 3)

data.dtype

dtype('float64')

# creating arrays

data1 = [6, 7.5, 8, 0, 1]

arr1 = np.array(data1)

arr1

array([6. , 7.5, 8. , 0. , 1. ])

data2 = [[1, 2, 3, 4], [5, 6, 7, 8]]

arr2 = np.array(data2)

arr2

array([[1, 2, 3, 4],
       [5, 6, 7, 8]])

arr2.ndim

arr2.shape

(2, 4)

arr1.dtype

dtype('float64')

arr2.dtype

dtype('int32')

np.zeros(10)

array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

np.ones((3, 6))

array([[1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1.]])

np.empty((2, 3, 2))

np.arange(15)

array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14])

data types for ndarrays

arr = np.array([1, 2, 3, 4, 5])

arr.dtype

dtype('int32')

float_arr = arr.astype(np.float64)

float_arr.dtype

dtype('float64')

int_array = np.arange(10)

calibers = np.array([.22, .27, .357, .380, .44, .50], dtype = np.float64)

int_array.astype(calibers.dtype)

array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

arithmetic with numpy arrays

arr = np.array([[1., 2., 3.], [4., 5., 6.]])

arr

array([[1., 2., 3.],
       [4., 5., 6.]])

arr * arr

array([[ 1.,  4.,  9.],
       [16., 25., 36.]])

arr + arr

array([[ 2.,  4.,  6.],
       [ 8., 10., 12.]])

1 / arr

array([[1.        , 0.5       , 0.33333333],
       [0.25      , 0.2       , 0.16666667]])

arr ** 2

array([[ 1.,  4.,  9.],
       [16., 25., 36.]])

# comparions between arrays yield boolean arrays

arr2 = np.array([[0, 4, 1], [7, 2., 12]])


arr2

array([[ 0.,  4.,  1.],
       [ 7.,  2., 12.]])

arr2 > arr

array([[False,  True, False],
       [ True, False,  True]])

basic indexing and slicing


arr = np.arange(10)

arr

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

arr[5]

arr[5:8]

array([5, 6, 7])

arr[5:8]

array([5, 6, 7])

arr

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

arr_slice= arr[5:8]


arr_slice

array([5, 6, 7])

 # changing values
arr_slice[1] = 12345

arr

array([    0,     1,     2,     3,     4,     5, 12345,     7,     8,
           9])

arr_slice

array([    5, 12345,     7])

# bare slice

arr_slice[:] = 64   #assigns all values to the array

arr

array([ 0,  1,  2,  3,  4, 64, 64, 64,  8,  9])

arr2d = np.array([[1,2,3], [4,5,6], [7,8,9]])

arr2d

array([[[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]]])

arr2d[1]

array([4, 5, 6])

arr2d[0][2]  #first array third element

arr2d[0,2]  # same result

arr3d = np.array([[[1,2,3], [4,5,6]], [[7,8,9], [10, 11, 12]]])

arr3d

array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

arr3d[0]

array([[1, 2, 3],
       [4, 5, 6]])

# scalar and vector arays can be assigned to arr3d[0]

old_values = arr3d[0].copy()

arr3d[0] = 42

arr3d

array([[[42, 42, 42],
        [42, 42, 42]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

arr3d[0] = old_values

arr3d

array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

arr3d[1,0]

array([7, 8, 9])

x = arr3d[1]

array([[ 7,  8,  9],
       [10, 11, 12]])

x[0]

array([7, 8, 9])

indexing with slices

arr

array([ 0,  1,  2,  3,  4, 64, 64, 64,  8,  9])

arr[1:6]

array([ 1,  2,  3,  4, 64])

# slicing a 2d array

arr2d

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

arr2d[:2] #selects the first two rows

array([[1, 2, 3],
       [4, 5, 6]])

arr2d[:2, 1:] #selects first two rows and last two columns

array([[2, 3],
       [5, 6]])

lower_dim_slice = arr2d[1, :2]
lower_dim_slice

array([4, 5])

lower_dim_slice.shape

(2,)

arr2d[:2, 2] #dots before selects rows before

array([3, 6])

arr2d[:, :1] #all rows, first column

array([[1],
       [4],
       [7]])

# assigning value to the section

arr2d[:2, 1:] = 0

arr2d

array([[1, 0, 0],
       [4, 0, 0],
       [7, 8, 9]])

Boolean indexing

names = np.array(['bob', 'joe', 'will','zhou', 'lu', 'wei' ])

names

array(['bob', 'joe', 'will', 'zhou', 'lu', 'wei'], dtype='<U4')

data = np.array([[4,7], [0,2], [-5, 6], [0, 0], [1, 2], [-12, -4], [3, 4]])
                 
data

array([[  4,   7],
       [  0,   2],
       [ -5,   6],
       [  0,   0],
       [  1,   2],
       [-12,  -4],
       [  3,   4]])

data.shape

(7, 2)

names.shape

(6,)

# let's check how many times wei's name come

names == 'wei'   #once

array([False, False, False, False, False,  True])

data[names == "wei"]

IndexError: boolean index did not match indexed array along dimension 0; dimension is 7 but corresponding boolean dimension is 6

# adding a name so that the dimension becomes 7
names = np.append(names, 'rajwinder')

names

array(['bob', 'joe', 'will', 'zhou', 'lu', 'wei', 'rajwinder',
       'rajwinder'], dtype='<U9')

# deleting extra

names = np.delete(names, 7)

names

array(['bob', 'joe', 'will', 'zhou', 'lu', 'wei', 'rajwinder'],
      dtype='<U9')

data[names == 'rajwinder']

array([[3, 4]])

data[names == 'zhou']

array([[0, 0]])

Fancy indexing

indexing using integers
indexing gets modified

arr = np.zeros((8, 4))


for i in range(8):
    arr[i] = i

arr

array([[0., 0., 0., 0.],
       [1., 1., 1., 1.],
       [2., 2., 2., 2.],
       [3., 3., 3., 3.],
       [4., 4., 4., 4.],
       [5., 5., 5., 5.],
       [6., 6., 6., 6.],
       [7., 7., 7., 7.]])

# selecting rows in particular order
arr[[4,3, 0, 6]]

array([[4., 4., 4., 4.],
       [3., 3., 3., 3.],
       [0., 0., 0., 0.],
       [6., 6., 6., 6.]])

# using negative indices
arr[[-2, -4, -7]]

array([[6., 6., 6., 6.],
       [4., 4., 4., 4.],
       [1., 1., 1., 1.]])

# multiple array indexing

arr3 = np.arange(32).reshape((8, 4))


arr3

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19],
       [20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])

# selecting elements based on rows and columns

arr3[[1, 4, 7, 2], [0, 3, 2, 1]]

array([ 4, 19, 30,  9])

# selecting complete rows and decding sequence of elements

arr3[[1, 4, 7, 2]][:, [0, 3, 2, 1]]

array([[ 4,  7,  6,  5],
       [16, 19, 18, 17],
       [28, 31, 30, 29],
       [ 8, 11, 10,  9]])

Transposing arrays and swapping axes

arr = np.arange(15). reshape(3, 5)
arr

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

arr.T

array([[ 0,  5, 10],
       [ 1,  6, 11],
       [ 2,  7, 12],
       [ 3,  8, 13],
       [ 4,  9, 14]])

# used often for matrix computation

arr

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

# multiplied two arrays
np.dot(arr.T, arr)

array([[125, 140, 155, 170, 185],
       [140, 158, 176, 194, 212],
       [155, 176, 197, 218, 239],
       [170, 194, 218, 242, 266],
       [185, 212, 239, 266, 293]])

# another way to do it
arr.T @ arr

array([[125, 140, 155, 170, 185],
       [140, 158, 176, 194, 212],
       [155, 176, 197, 218, 239],
       [170, 194, 218, 242, 266],
       [185, 212, 239, 266, 293]])

arr

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

arr.swapaxes(0, 1)  # returns the view without making a copy

array([[ 0,  5, 10],
       [ 1,  6, 11],
       [ 2,  7, 12],
       [ 3,  8, 13],
       [ 4,  9, 14]])

Pseudorandom number generation

samples = np.random.standard_normal(size= (4, 4))

samples

array([[ 0.26762709, -0.62405293,  0.67249719, -0.46023273],
       [ 0.40611368, -0.01041362,  0.51275103, -1.95844566],
       [ 0.90884576, -0.28283029,  0.47254105,  2.20649657],
       [ 0.69228499, -0.31918775, -0.74474035,  0.28790593]])

rng = np.random.default_rng(seed = 12334)

data = rng.standard_normal((2,3))

type(rng)

numpy.random._generator.Generator

Universal Functions : Fast Element-Wise Array Functions

import numpy as np
from random import normalvariate
arr = np.arange(10)

np.sqrt(arr)

array([0.        , 1.        , 1.41421356, 1.73205081, 2.        ,
       2.23606798, 2.44948974, 2.64575131, 2.82842712, 3.        ])

np.exp(arr)

array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
       5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
       2.98095799e+03, 8.10308393e+03])

x = rng.standard_normal(8)

y = rng.standard_normal(8)

x

array([-0.32357072, -1.8494368 , -1.89739205,  0.04315429,  1.01046514,
       -0.73625393,  0.46616191, -0.09290374])

array([-0.12705798, -0.64476954, -0.62430977,  0.87432098,  1.55273649,
       -1.53739177, -0.73752509,  0.41995739])

np.maximum(x, y)  #based on element wise comparison

array([-0.12705798, -0.64476954, -0.62430977,  0.87432098,  1.55273649,
       -0.73625393,  0.46616191,  0.41995739])

arr = rng.standard_normal(7) * 5

arr

array([-1.61785359, -9.24718402, -9.48696026,  0.21577147,  5.05232568,
       -3.68126964,  2.33080955])

remainder, whole_part = np.modf(arr)

remainder

array([-0.61785359, -0.24718402, -0.48696026,  0.21577147,  0.05232568,
       -0.68126964,  0.33080955])

whole_part

array([-1., -9., -9.,  0.,  5., -3.,  2.])

arr

array([-1.61785359, -9.24718402, -9.48696026,  0.21577147,  5.05232568,
       -3.68126964,  2.33080955])

out = np.zeros_like(arr)

np.add(arr, 1)

array([-0.61785359, -8.24718402, -8.48696026,  1.21577147,  6.05232568,
       -2.68126964,  3.33080955])

np.add(arr, 1, out= out)

array([-0.61785359, -8.24718402, -8.48696026,  1.21577147,  6.05232568,
       -2.68126964,  3.33080955])

out

array([-0.61785359, -8.24718402, -8.48696026,  1.21577147,  6.05232568,
       -2.68126964,  3.33080955])

Array oriented programming with Arrays

vectorization (faster) than pure Python equivalents

points = np.arange(-5, 5, 0.01) #100 equally spaced points

xs, ys = np.meshgrid(points, points)

# numpy.meshgrid function takes two one-dimensional arrays and produces two two-dimensional matrices


ys

array([[-5.  , -5.  , -5.  , ..., -5.  , -5.  , -5.  ],
       [-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
       [-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
       ...,
       [ 4.97,  4.97,  4.97, ...,  4.97,  4.97,  4.97],
       [ 4.98,  4.98,  4.98, ...,  4.98,  4.98,  4.98],
       [ 4.99,  4.99,  4.99, ...,  4.99,  4.99,  4.99]])

z = np.sqrt (xs ** 2 + ys ** 2)

z

array([[7.07106781, 7.06400028, 7.05693985, ..., 7.04988652, 7.05693985,
        7.06400028],
       [7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
        7.05692568],
       [7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
        7.04985815],
       ...,
       [7.04988652, 7.04279774, 7.03571603, ..., 7.0286414 , 7.03571603,
        7.04279774],
       [7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
        7.04985815],
       [7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
        7.05692568]])

# visualizations with 2-d arrays

import matplotlib.pyplot as plt

plt.imshow(z, cmap = plt.cm.gray, extent = [-5, 5, -5, 5])

plt.colorbar()

plt.title("Image plot $\sqrt{x^2 + y^2}$ for a grid of values")

Text(0.5, 1.0, 'Image plot $\\sqrt{x^2 + y^2}$ for a grid of values')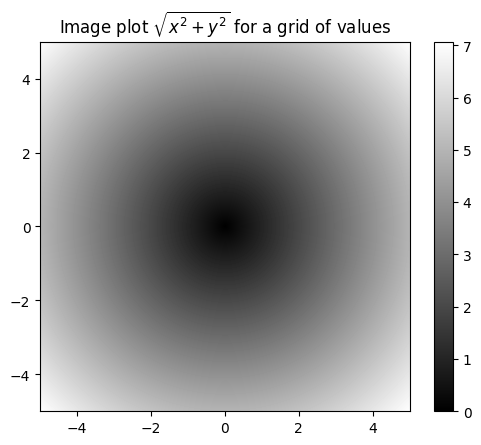

plt.close('all')

Expressing Conditional Logic as Array Operations

xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])

yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])

cond = np.array([True, False, True, True, False])

# take value form xarr whenever true, otherwise take value from yarr

result = [(x if c else y)
         for x, y, c in zip (xarr, yarr, cond)]

result

[1.1, 2.2, 1.3, 1.4, 2.5]

numpy.where

# numpy.where (replace all positive values with 2 and negative with -2)

arr = rng.standard_normal((4, 4))

arr

array([[-0.09290374, -0.12705798, -0.64476954, -0.62430977],
       [ 0.87432098,  1.55273649, -1.53739177, -0.73752509],
       [ 0.41995739, -0.93658739,  0.62072248,  0.81057914],
       [-0.21398203,  0.67748945, -1.54002066, -0.9638457 ]])

arr > 0

array([[False, False, False, False],
       [ True,  True, False, False],
       [ True, False,  True,  True],
       [False,  True, False, False]])

np.where (arr  > 0, 2, -2)

array([[-2, -2, -2, -2],
       [ 2,  2, -2, -2],
       [ 2, -2,  2,  2],
       [-2,  2, -2, -2]])

# or set only the positive values to 2

np.where (arr > 0, 2, arr)

array([[-0.09290374, -0.12705798, -0.64476954, -0.62430977],
       [ 2.        ,  2.        , -1.53739177, -0.73752509],
       [ 2.        , -0.93658739,  2.        ,  2.        ],
       [-0.21398203,  2.        , -1.54002066, -0.9638457 ]])

mathematical and statistical methods

arr = rng.standard_normal ((5, 4))

arr

array([[-0.64316368, -0.48860061, -1.41271857, -0.10120962],
       [-0.70385422,  2.41319157, -0.54405393, -0.90339244],
       [ 0.82712685, -0.62647321, -0.13480887,  0.03956079],
       [ 0.56044129,  0.34237924, -0.6576538 ,  1.04696188],
       [ 0.17595271, -1.13639865, -0.54922125,  0.70725439]])

arr.mean()

-0.08943400646176203

np.mean(arr)

-0.08943400646176203

arr.sum()

-1.7886801292352406

arr.mean(axis = 1) # columns

array([-0.66142312,  0.06547274,  0.02635139,  0.32303215, -0.2006032 ])

arr.sum(axis = 1)

array([-2.64569248,  0.26189098,  0.10540556,  1.29212861, -0.8024128 ])

arr = np.array([0,1,2,3,4,5,6,7])

arr.cumsum()

array([ 0,  1,  3,  6, 10, 15, 21, 28])

arr = np.array([[0,1,2], [3, 4, 5], [6, 7, 8]])


arr

array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

# arr.cumsum(axis = 0 ) computes the cumulative sum along rows

# arr.sumsum (axis= 1) computes the sum along columns

arr.cumsum(axis = 0)

array([[ 0,  1,  2],
       [ 3,  5,  7],
       [ 9, 12, 15]])

arr.cumsum(axis = 1)

array([[ 0,  1,  3],
       [ 3,  7, 12],
       [ 6, 13, 21]])

methods for boolean arrays

arr = rng.standard_normal(100)

(arr> 0).sum()

(arr <= 0).sum()   #all non-po

Sorting

arr = rng.standard_normal(6)

arr

array([ 0.81272428, -0.67629236,  0.09344394, -0.20621744,  0.10364886,
        0.70966403])

arr.sort()

arr

array([-0.67629236, -0.20621744,  0.09344394,  0.10364886,  0.70966403,
        0.81272428])

arr = rng.standard_normal((5, 3))

arr

array([[-1.58684863, -0.1143117 ,  2.38420916],
       [-0.64811009,  1.31931176,  0.01123432],
       [-0.90663373, -0.96531814,  0.46431808],
       [ 0.52164015, -0.08486576, -0.98397298],
       [ 0.09054187, -1.08417551, -0.48832961]])

arr.sort (axis = 0)  #sorts the values across columns

arr

array([[-1.58684863, -1.08417551, -0.98397298],
       [-0.96531814, -0.90663373, -0.48832961],
       [-0.64811009, -0.1143117 ,  0.01123432],
       [-0.08486576,  0.09054187,  0.46431808],
       [ 0.52164015,  1.31931176,  2.38420916]])

arr.sort (axis = 1) 

arr

array([[-1.58684863, -1.08417551, -0.98397298],
       [-0.96531814, -0.90663373, -0.48832961],
       [-0.64811009, -0.1143117 ,  0.01123432],
       [-0.08486576,  0.09054187,  0.46431808],
       [ 0.52164015,  1.31931176,  2.38420916]])

arr2 = np.array([5, -10, 7, 1, 0, -3])


sorted_arr2 = np.sort(arr2)

sorted_arr2

array([-10,  -3,   0,   1,   5,   7])

unique and other set logic

names

array(['bob', 'joe', 'will', 'zhou', 'lu', 'wei', 'rajwinder'],
      dtype='<U9')

np.unique(names)

array(['bob', 'joe', 'lu', 'rajwinder', 'wei', 'will', 'zhou'],
      dtype='<U9')

np.append(names, 'lu')

array(['bob', 'joe', 'will', 'zhou', 'lu', 'wei', 'rajwinder', 'lu'],
      dtype='<U9')

# we've 'lu' twice now, let's see now unique

# sorting done aswell

np.unique(names)

array(['bob', 'joe', 'lu', 'rajwinder', 'wei', 'will', 'zhou'],
      dtype='<U9')

# python alternative

sorted(set(names))

['bob', 'joe', 'lu', 'rajwinder', 'wei', 'will', 'zhou']

array set operations

# numpy.in1d for testing memebership of the values in one array

values = np.array([6, 0,0,0,3,2])

np.in1d(values, [1,2,3])

array([False, False, False, False,  True,  True])

file input and output

arr = np.arange(10)

np.save('some_array', arr)

np.load('some_array.npy')

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# save multiple arrays using  np.savez
np.savez('array_archive.npz', a = arr, b=arr)

arch = np.load("array_archive.npz")

arch['b']

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# saving in compressed format

np.savez_compressed('arrays_compressed.npz', a= arr, b= arr)

Linear Alzerba

x = np.array([[1, 2, 3], [4, 5, 6]])

y = np.array([[6, 23], [-1, 7], [8,9]])

x

array([[1, 2, 3],
       [4, 5, 6]])

array([[ 6, 23],
       [-1,  7],
       [ 8,  9]])

x.dot(y)

array([[ 28,  64],
       [ 67, 181]])

# equivalent to

np.dot(x, y)

array([[ 28,  64],
       [ 67, 181]])

# product of 1d and 2d array
x @ np.ones(3)

array([ 6., 15.])

# numpy.linalg (matrix decompositions)

from numpy.linalg import inv, qr

X = rng.standard_normal((5, 5))

mat = X.T @ X

mat

array([[ 5.79511464, -3.30831545, -2.66542844, -0.61858429, -4.34315368],
       [-3.30831545,  6.04913293,  1.09484984, -0.88187098,  3.79344801],
       [-2.66542844,  1.09484984,  3.59693921, -0.10949232,  1.50109261],
       [-0.61858429, -0.88187098, -0.10949232,  0.68764721,  0.24806815],
       [-4.34315368,  3.79344801,  1.50109261,  0.24806815,  4.09980802]])

inv(mat)

array([[ 1.95391205,  0.4259796 ,  0.86161239,  1.99396982,  1.23962108],
       [ 0.4259796 ,  1.84110512,  0.55359754,  3.43225775, -1.66263314],
       [ 0.86161239,  0.55359754,  0.79117237,  1.60608307,  0.01366661],
       [ 1.99396982,  3.43225775,  1.60608307,  8.69084511, -2.17736422],
       [ 1.23962108, -1.66263314,  0.01366661, -2.17736422,  3.22224774]])

mat @ inv(mat)

array([[ 1.00000000e+00,  7.37690538e-17,  8.63526934e-17,
         2.45602532e-16,  5.57110698e-16],
       [ 3.59505366e-17,  1.00000000e+00, -1.43602651e-16,
         1.56181454e-15, -8.26684003e-16],
       [-2.51848975e-16, -9.56323491e-18,  1.00000000e+00,
        -7.81952475e-16, -4.32942875e-16],
       [-1.22081410e-16,  5.77266093e-17, -3.23653576e-16,
         1.00000000e+00, -9.26541377e-18],
       [-4.93401745e-16,  1.63171237e-15, -7.64319458e-17,
         1.26774536e-15,  1.00000000e+00]])

Random walks

# with python

import random
position = 0
walk = [position]
nsteps = 1000

for _ in range(nsteps):
    step = 1 if random.randint(0, 1) else -1
    position += step
    walk.append (position)

plt.plot(walk[:100])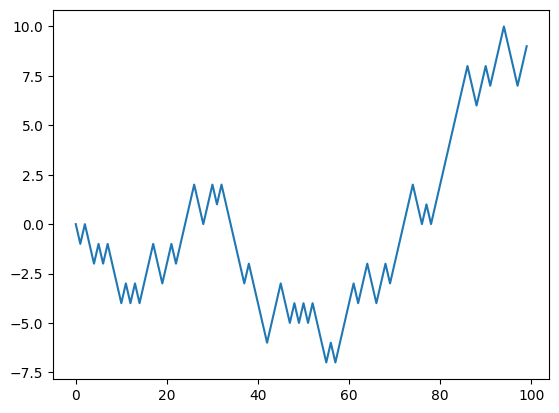

# with numpy

nsteps = 1000

rng = np.random.default_rng (seed = 12345)

draws = rng.integers(0, 2, size= nsteps)
steps = np.where(draws == 0, 1, -1)

walk = steps.cumsum()

walk.min()

-8

walk.max()

(np.abs(walk) >= 10).argmax()

# simulting many random walks at once with numpy


nwalks = 5000

nsteps = 1000

draws = rng.integers(0, 2, size = (nwalks, nsteps))

steps = np.where(draws > 0, 1, -1)

walks = steps.cumsum(axis = 1)

walks

array([[  1,   2,   1, ..., -24, -25, -26],
       [ -1,   0,  -1, ...,  -2,  -1,   0],
       [  1,   0,   1, ..., -22, -23, -24],
       ...,
       [  1,   0,   1, ...,   0,   1,   0],
       [ -1,  -2,  -3, ...,  78,  77,  78],
       [  1,   2,   1, ..., -42, -41, -40]])

walks.max()

walks.min()

-125

# any method to check for details

hits30 = (np.abs(walks) >=30).any(axis = 1)

hits30

array([ True, False,  True, ..., False,  True,  True])

hits30.sum()

crossing_times = (np.abs(walks[hits30]) >= 30).argmax(axis = 1)

crossing_times

array([897, 187, 607, ..., 497, 363, 337], dtype=int64)

# average minn